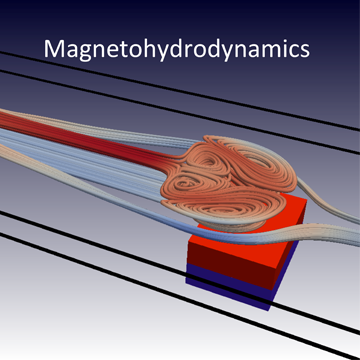
Convection processes can be found almost everywhere. Think of air condition systems in buildings, the generation of magnetic fields in the Earth and Sun, or the formation of clouds in the atmosphere. The figure is a view from the top onto a cylindrical Rayleigh-Benard convection cell, one of the simplest convection systems. The streamlines of the instantaneous velocity field are plotted. They indicate a complex large-scale circulation pattern which evolves in convective turbulence. One of the big miracles in convection is how these patterns grow out of the stochastic turbulent fluid motion and how they affect the turbulent heat transport through the cell. A way to attempt this problem is by a drastic reduction of the degrees of freedom in the underlying mathematical model. Such a so-called low-dimensional system can then be analysed with very powerful instruments of the theory of dynamical systems.
Furthermore, we study the impact of moisture on thermal convection which allows for additional condensation and evaporation. This aspect is important for a better understanding of the formation, shape and lifetime of atmospheric clouds.
Current Collaborations:
Janet D. Scheel (Occidental College Los Angeles),
Raymond A. Shaw (Michigan Technological University Houghton),
Olivier Pauluis (Courant Institute for Mathematical Sciences, New York University),
Katepalli R. Sreenivasan (Tandon School of Engineering, New York University)